定义
相对于普通队列的先进先出,优先队列则是具有最高优先级的元素先出
底层数据结构
通常用过堆来实现
堆
堆是一个可以被看做一棵树的数组对象。并且满足下列性质:
- 堆总是一棵完全二叉树
- 堆中某个节点的值总是不大于(不小于)其父节点的值
其中,堆中某个节点的值总是不大于其父节点的值称为最大堆,反之为最小堆
堆的抽象结构(二叉树)与实际存储结构(数组)
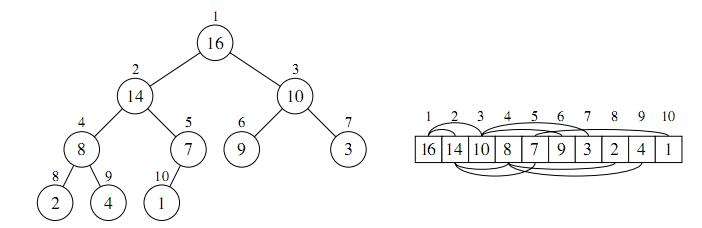
抽象二叉树结构节点间的关系在实际数组结构中的映射
设当前节点的索引为n , 堆大小为 m
- 获取左子节点的索引 left = 2*n + 1
- 获取右子节点的索引 right = 2*n + 2 = left + 1
- 获取父节点的索引 parent = (n - 1) / 2
- 获取最后一个非叶子节点 index = m / 2
上浮节点
设当前需要上浮的节点索引为n,比较当前节点与其父节点,若当前节点大于其父节点,则将当前节点与其父节点交换。重复以上操作,直到该节点小于其父节点,或已是根节点
下沉节点
设当前需要下沉的节点索引为n,比较当前节点与其左右子节点中最大值,若小于其左右子节点中最大值,则将当前节点与其左右子节点中最大值节点交换。重复以上操作,直到该节点大于其左右子节点,或者已是叶子节点
删除节点
将堆中最后一个节点覆盖需要删除的节点,之后下沉覆盖后的新节点
插入新节点
将新节点放到堆的最后,之后上浮新节点
堆化数组
依次下沉从最后一个非叶子节点到根节点的所有节点
通过堆实现优先队列
优先队列初始化
- 最大堆化初始的无序元素数组
出队
- 取出并删除最大堆根节点元素(最高优先级)
入队
- 向最大堆中插入新元素
代码
public class PriorityQueue<T> {
private int size;
private final int DEFAULT_SIZE = 11;
private Object[] queue;
private Comparator<T> comparator;
public boolean offer(T t){
size++;
if (size > queue.length) grow();
queue[size - 1] = t;
siftUp(size - 1);
return true;
}
@SuppressWarnings("unchecked")
public T peek(){
return size == 0 ? null : (T) queue[0];
}
@SuppressWarnings("unchecked")
public T poll(){
T res = peek();
if (res != null){
int s = --size;
T tail = (T) queue[s];
queue[s] = null;
if (s != 0) {
queue[0] = tail;
siftDown(0);
}
}
return res;
}
public void remove(T t){
int index = indexOf(t);
exchange(index, --size);
queue[size] = null;
siftDown(index);
}
public void clear(){
for (int i = 0; i < size; i++)
queue[i] = null;
size = 0;
}
public PriorityQueue(int capacity, Comparator<T> comparator){
this.queue = new Object[capacity];
this.comparator = comparator;
}
public PriorityQueue(Comparator<T> comparator){
this.queue = new Object[DEFAULT_SIZE];
this.comparator = comparator;
}
public PriorityQueue(Object[] array, Comparator<T> comparator){
this.size = array.length;
this.comparator = comparator;
queue = Arrays.copyOf(array, array.length << 1);
heapify();
}
private void grow(){
int oldCapacity = queue.length;
int newCapacity = oldCapacity << 1;
queue = Arrays.copyOf(queue, newCapacity);
}
private void heapify(){
if(size <= 1) return;
for (int i = (size - 1) >> 1; i >= 0; i--) {
siftDown(i);
}
}
@SuppressWarnings("unchecked")
private void siftUp(int index){
int current = index;
int father;
while (current != 0){
father = (current - 1) >> 1;
if (comparator.compare((T) queue[current], (T) queue[father]) > 0){
exchange(father, current);
}
current = father;
}
}
@SuppressWarnings("unchecked")
private void siftDown(int index){
int leftSon, rightSon;
int root = index;
while ((leftSon = (root << 1) + 1) < size) {
rightSon = leftSon + 1;
int prioritySon = leftSon;
if (rightSon < size &&
comparator.compare((T) queue[rightSon], (T) queue[leftSon]) > 0){
prioritySon = rightSon;
}
if (comparator.compare((T) queue[prioritySon], (T) queue[root]) > 0) {
exchange(root, prioritySon);
}
root = prioritySon;
}
}
private void exchange(int index1, int index2){
Object tmp = queue[index1];
queue[index1] = queue[index2];
queue[index2] = tmp;
}
private int indexOf(T t){
for (int i = 0; i < size; i++) {
if (queue[i] == t) return i;
}
return -1;
}
}
下篇延迟队列